Gradient Descent is a method used to find the minimum of a function. Imagine walking downhill towards the lowest point in a valley—that's what this method does mathematically. It calculates the gradient (the slope) of the function and takes steps in the direction that decreases the function's value. It's powerful for optimizing in machine learning and economics. However, it struggles with functions having many valleys (local minima) or plateaus, and might not find the absolute lowest point (global minimum).

Linear Programming (LP) is a mathematical method used to find the best outcome in a model whose requirements are represented by linear relationships. It's like playing a game where you need to achieve the highest score (maximize) or the lowest score (minimize) under certain rules. These rules are your constraints, like how much money you can spend or how many hours you have. The score you're trying to optimize is called the objective function, and it's also a linear equation. LP helps you figure out the best way to play this game, balancing all the rules, to achieve your goal, whether it's making the most profit, using the least resources, or something similar. It's a powerful tool for decision-making in business, engineering, economics, and more.

Imagine you have a map with various paths and you need to find the shortest way to a treasure. Each path has its own rules, like how much weight you can carry or how fast you can travel. The Simplex algorithm helps you navigate these paths and rules to find the most efficient route to the treasure.

In technical terms, it deals with equations representing constraints (like the rules of each path) and a goal (like reaching the treasure in the shortest time). The algorithm iteratively explores vertices on a multidimensional shape (the map), checking at each step if it's closer to the best solution. It's like checking each intersection on a map to see if you're closer to the treasure. This continues until it finds the most efficient route, giving you the best solution to your problem.

This project’s main goal is a linear programming model that re-envisions ambitious yet feasible renewable energy goals for key regions by focusing on the trade-offs between different fossil-free energy sources.  For this, the project focuses on the data of four common fossil-free energy sources: wind, solar, nuclear and hydro, as well as relevant variables such as Cost, Reliability, Existing Energy Mix and Public Approval.

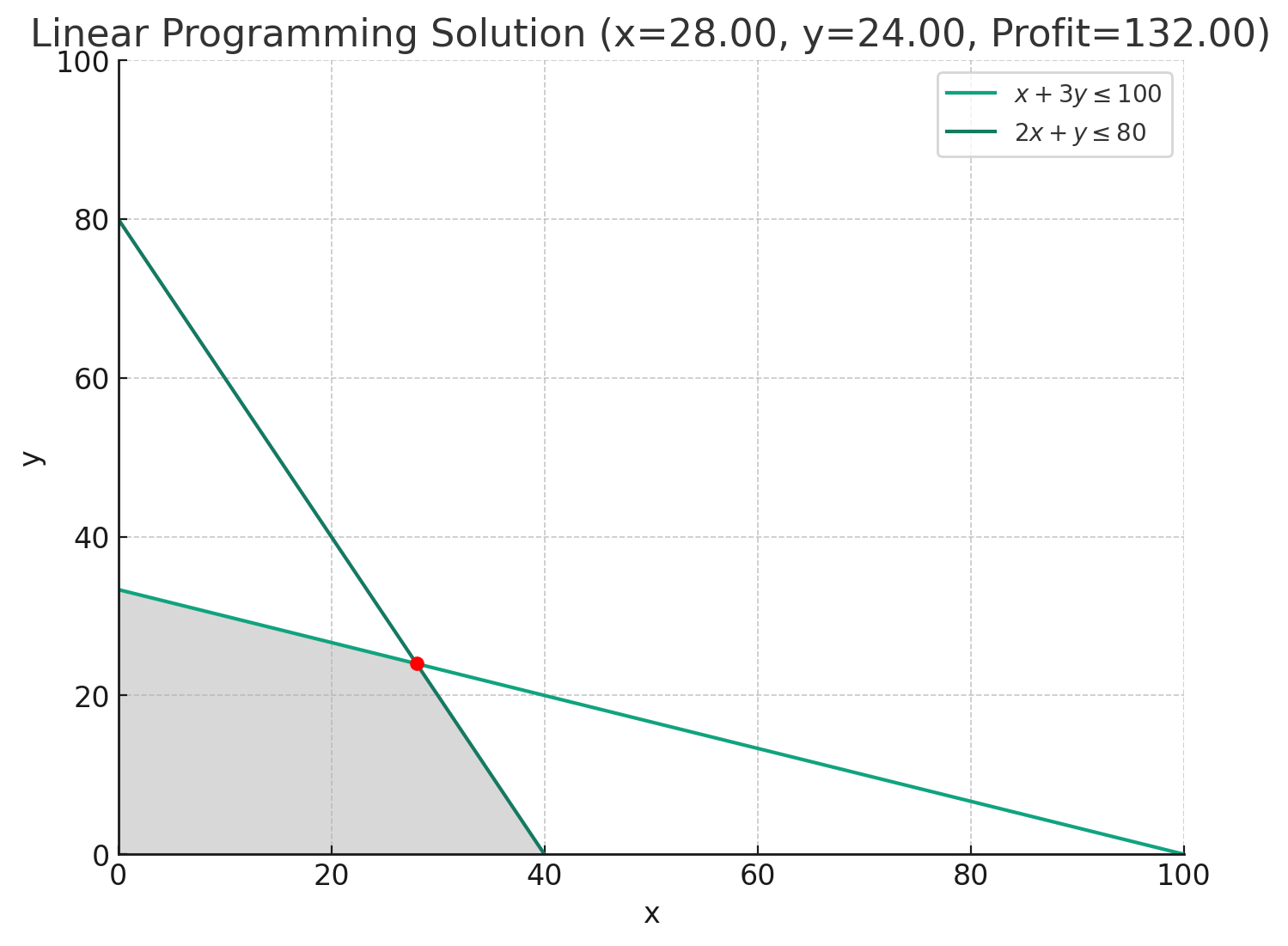
Focus: LP deals specifically with linear equations and inequalities. This means it works with problems where relationships are represented as straight lines (hence 'linear').

Objective: It always aims to find the maximum or minimum value of a linear equation, known as the objective function. For example, maximizing profit or minimizing cost.

Method: LP uses specific mathematical methods, like the Simplex algorithm, to find the best solution.

Constraints: All constraints in LP are linear (straight-line relationships). For instance, you can't spend more than a certain budget, or you need at least a certain amount of some ingredient.

Solutions: Solutions in LP are often numerical and can include fractions or decimals.

Diet Problem (DP) involves finding the most cost-effective diet that meets all nutritional requirements. Imagine you have a list of foods, each with its own nutritional content and cost. Your goal is to choose a combination of these foods that provides all the necessary nutrients (like vitamins, proteins, carbohydrates, etc.) for the least possible cost. You set up equations for each nutrient, ensuring your diet doesn't fall short or exceed what's needed. Then, you use linear programming to minimize the total cost while satisfying these nutritional constraints. It's like solving a puzzle where you balance your health needs against your budget, finding the best possible dietary plan.

Here is a CSV containing information about nutritive values of different vegetables growable in a German garden, last column also contains expected yield per square meter. Please provide a combination of vegetables which would satisfy nutritive need of an adult man so that the surface on which the vegetables grow is minimized. To have the meal diversified, there should be not more than 300g of certain vegetable.

The 3-SAT (3-Satisfiability) problem is a classic question in computer science and mathematical logic. It's a specific type of Boolean satisfiability problem. In 3-SAT, you're given a formula composed of several clauses, where each clause is a disjunction (an "OR" operation) of exactly three literals (variables or their negations). The challenge is to determine if there exists an assignment of truth values (true or false) to the variables that makes the entire formula true. This problem is known for being NP-complete, meaning it's easy to check a solution but potentially very hard to find one, especially as the number of variables increases. This characteristic makes 3-SAT important in theoretical computer science, particularly in studies related to computational complexity.